Rumus Persamaan Kuadrat Beserta Pengertian, Contoh Soal dan Penjelasannya

JAKARTA, iNews.id - Apa kalian tahu rumus persamaan kuadrat dan bagaimana menghitung persamaan kuadrat tersebut? Agar semakin paham, pelajari informasinya di sini.

Persamaan kuadrat merupakan suatu persamaan yang di mana pangkat tertinggi dan variabelnya adalah dua. Bentuk umum persamaan kuadrat adalah ax2 + bx + c = 0 dengan a ≠ 0, a, b, c, € R dan a ≠ 0

Baca Juga

Putin Ledek Zelensky karena Selfie di Kupiansk: Dia Artis Berbakat!

Dalam persamaan kuadrat ax2 + bx + c = 0, a disebut koefisien x2, b disebut koefisien x, dan c disebut konstanta atau terapan. Beberapa persamaan kuadrat memiliki bentuk baku. Selain itu, terdapat pula bentuk-bentuk persamaan kuadrat yang tidak baku, seperti :

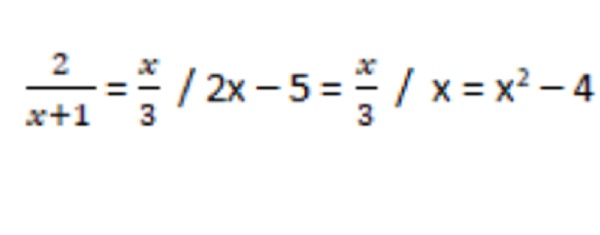
Persamaan kuadrat tidak baku tersebut dapat diubah menjadi bentuk baku dengan sedikit manipulasi aljabar. Persamaan-persamaan kuadrat tadi menggunakan x sebagai variabelnya. Persamaan kuadrat dapat pula menggunakan variabel lain. Seperti, P2 - 3p – 5 = 0 adalah persamaan kuadrat dalam p dan 3t2 – 5t + 7 = 0 adalah persamaan kuadrat dalam t.

Baca Juga

11 Contoh Soal Bilangan Bulat Matematika Beserta Pengertian, Rumus dan Sifatnya

Cara Menyelesaikan Permasalahan Kuadrat

Nah, untuk menyelesaikan soal persamaan kuadrat, ada tiga rumus yang bisa digunakan, yakni sebagai berikut:

Baca Juga

Latihan Soal Matematika Kelas 6 Semester 1 Beserta Kunci Jawabannya

• 1. Menyelesaikan Persamaan Kuadrat dengan Pemfaktoran

Rumus persamaan kuadrat pemfaktoran 
a(x – x1) (x – x2) = 0

Contoh Soal :

Tentukan himpunan penyelesaian persamaan kuadrat berikut ini dengan cara pemfaktoran dari x2 – 4x = 0 
 x2 – 4x = 0 -> x (x – 4) = 0
-> x = 0 atau x - 4 = 0
-> x = 0 atau x = 4

Jadi, akar persamaan kuadrat tersebut adalah x = 0  atau x = 4. Dengan kata lain, himpunan penyelesaian persamaan kuadrat tersebut adalah (0,4)

• 2. Melengkapkan kuadrat sempurna

Rumus persamaan kuadrat sempurna 

Contoh Soal : 

Tentukan himpunan penyelesaian persamaan kuadrat berikut dengan cara melengkapi bentuk kuadrat sempurna dari x2 + 2x – 3 = 0
x2 + 2x – 3 = 0 -> x2 + 2x = 3

Bentuk kuadrat x2 + 2x dapat diubah menjadi bentuk kuadrat sempurna dengan cara menentukan nilai konstanta sebagai kuadrat setengah koefisien x, yaitu (½ x 2)2 = 1, sehingga diperoleh : x2 + 2x = 3 -> x2 + 2x (½ x 2)3 = 3 + (½ x 2)2 
-> x2 +2x + 1 = 3 + 1
-> (x + 1)2 = 4
-> x + 1 = ± 
-> x + 1 = ± 2
-> x + 1 = -2 atau x + 1 = 2
-> x = -3 atau x = 1. Jadi, himpunan penyelesaiannya adalah (-3, 1)

• 3. Metode penyelesaian persamaan kuadrat dengan rumus kuadrat

Rumus Persamaan Kuadrat 

Dua akar persamaan kuadrat tersebut sering ditulis dengan

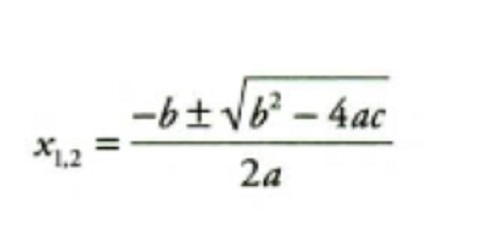
Contoh soal :

Tentukan himpunan penyelesaian persamaan kuadrat berikut dengan rumus kuadrat, yaitu  x2 - 4x - 5 = 0

Penyelesaian dengan rumus persamaan kuadrat:

Koefisien suku-suku persamaan kuadrat x2 - 4x - 5 = 0 adalah a = 1, b = 4, dan c = -5
 
(foto rumus persamaan kuadrat)
-> x1 = 2 -3 atau x2 = 2 + 3
-> x1 = -1 atau x2 = 5. Jadi, himpunan penyelesaiannya adalah (-1,5)

Itulah beberapa rumus persamaan kuadrat beserta dengan contoh soal yang dapat kalian pelajari di rumah dengan sendirinya. Semoga bermanfaat

Editor: Puti Aini Yasmin