5 Contoh Soal Permutasi Beserta Pembahasan Jawabannya

4. Permutasi jika diketahui ada n1 unsur yang sama, n2 unsur yang sama dan seterusnya sampai nk maka banyaknya permutasi adalah

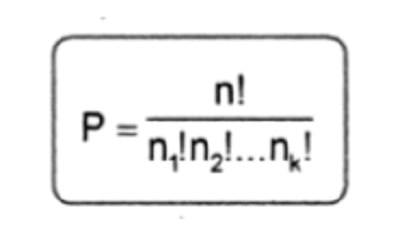
Keterangan:
P = Permutasi
n! = Jumlah benda faktorial
nk! = Jumlah unsur yang sama faktorial

Contoh soal permutasi:

Tentukan banyaknya permutasi pada kata MANTAN!

Jawab: 

Jadi, banyaknya permutasi adalah 180. 

5. Permutasi siklis, yakni permutasi yang letak elemen-elemennya tidak segaris, tetapi melingkar. 

Rumus permutasi:

P = (n-1)!

Contoh soal permutasi siklis beserta jawabannya

Dengan berapa cara 4 orang duduk pada 4 kursi di sebuah meja melingkar !

Jawab :
P = (n - 1)!
P = (4-1)!
   = 3!
P = 3.2.1
P = 6

6. Tentukan susunan dua huruf yang bisa dibuat dari huruf P, Q, dan R!

Jawaban

Dengan menggunakan metode himpunan pasangan berturut, maka diperoleh susunan huruf sebagai berikut: PQ, PR, QR, QP, RP, RQ, berjumlah 6 susunan.

Dengan menggunakan aturan permutasi, maka jumlah susunan dua huruf adalah

ₙPᵣ = n!/(n - r)!

₃P₂ = 3!/(3 - 2)!

= 3!/1!

= 3 x 2 x 1 = 6 susunan

6P3 = 6! Per (6 – 3)!

6P3 = (6 x 5 x 4 x 3!) / 3!

6P3 = 6 x 5 x 4

6P3 = 120.

Jadi, banyak bilangan yang dapat disusun, yaitu 120 bilangan.

7. Suatu kelompok belajar yang beranggotakan empat orang (A, B, C dan D) akan memilih ketua dan wakil ketua kelompok. Ada berapa alternatif susunan ketua dan wakil ketua dapat dipilih ?

Jawaban:

nPx = (n!)/(n-x)!

4P2 = (4!)/(4-2)!

= 12 cara (AB, AC, AD, BA, BC, BD, CA, CB, CD, DA, DB, DC) .

8. Terdapat tiga orang (X, Y dan Z) yang akan duduk bersama di sebuah bangku. Ada berapa urutan yang dapat terjadi ?

Jawaban:

nPx = n!

3P3 = 3!

= 1 x 2 x 3

= 6 cara (XYZ, XZY, YXZ, YZX, ZXY, ZYX).

8. Peluang lulusan PNJ dapat bekerja pada suatu perusahaan adalah 0,75. Jika seorang lulusan PNJ mendaftarkan pada 24 perusahaan, maka berapakah dia dapat diterima oleh perusahaan?

Pembahasan:

Frekuensi harapan kejadian A adalah Fh(A) = n × P(A)

Diketahui P(A) = 0,75 dan n = 24. Maka:

Fh(A) = 24 × 0,75 = 18 perusahaan.

9. Sekelompok mahasiswa yang terdiri dari 10 orang akan mengadakan rapat dan duduk mengelilingi sebuah meja, ada berapa carakah kelima mahasiswa tersebut dapat diatur pada sekeliling meja tersebut?

Pembahasan:

P5 = (10-1)!

= 9.8.7.6.5.4.3.2.1

= 362880 cara

10. Menjelang Pergantian kepengurusan BEM STMIK Tasikmalaya akan dibentuk panitia inti sebanyak 2 orang (terdiri dari ketua dan wakil ketua), calon panitia tersebut ada 6 orang yaitu: a, b, c, d, e, dan f. Ada berapa pasang calon yang dapat duduk sebagai panitia inti tersebut?

Pembahasan:

6P2 = 6!/(6-2)!

= (6.5.4.3.2.1)/(4.3.2.1)

= 720/24

= 30 cara

Demikian contoh soal permutasi dari 5 jenis permutasi. Meskipun sekilas terlihat susah namun jika dipelajari dengan baik, permutasi bisa dengan mudah dikerjakan. Selamat belajar!

Editor: Puti Aini Yasmin